Tooltips feel like the smallest UI problem you can have. They’re tiny and usually hidden. When someone asks how to build one, the traditional answer almost always comes back using some JavaScript library. And for a long time, that was the sensible advice.
I followed it, too.
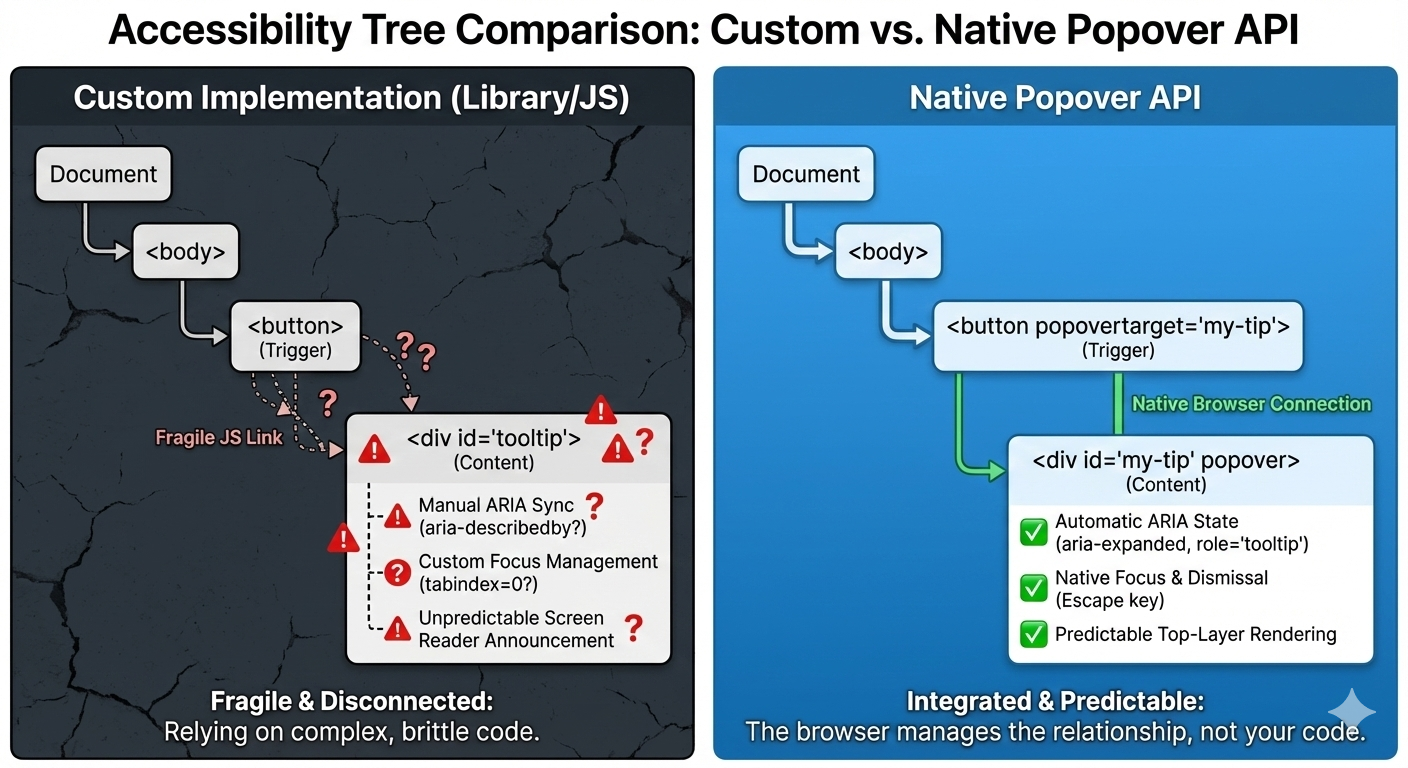
On the surface, a tooltip is simple. Hover or focus on an element, show a little box with some text, then hide it when the user moves away. But once you ship one to real users, the edges start to show. Keyboard users Tab into the trigger, but never see the tooltip. Screen readers announce it twice, or not at all. The tooltip flickers when you move the mouse too quickly. It overlaps content on smaller screens. Pressing Esc does not close it. Focus gets lost.
Over time, my tooltip code grew into something I didn’t really want to own anymore. Event listeners piled up. Hover and focus had to be handled separately. Outside clicks needed special cases. ARIA attributes had to be kept in sync by hand. Every small fix added another layer of logic.
Libraries helped, but they were also more like black boxes I worked around instead of fully understanding what was happening behind the scenes.
That was what pushed me to look at the newer Popover API. I wanted to see what would happen if I rebuilt a single tooltip using the browser’s native model without the aid of a library.
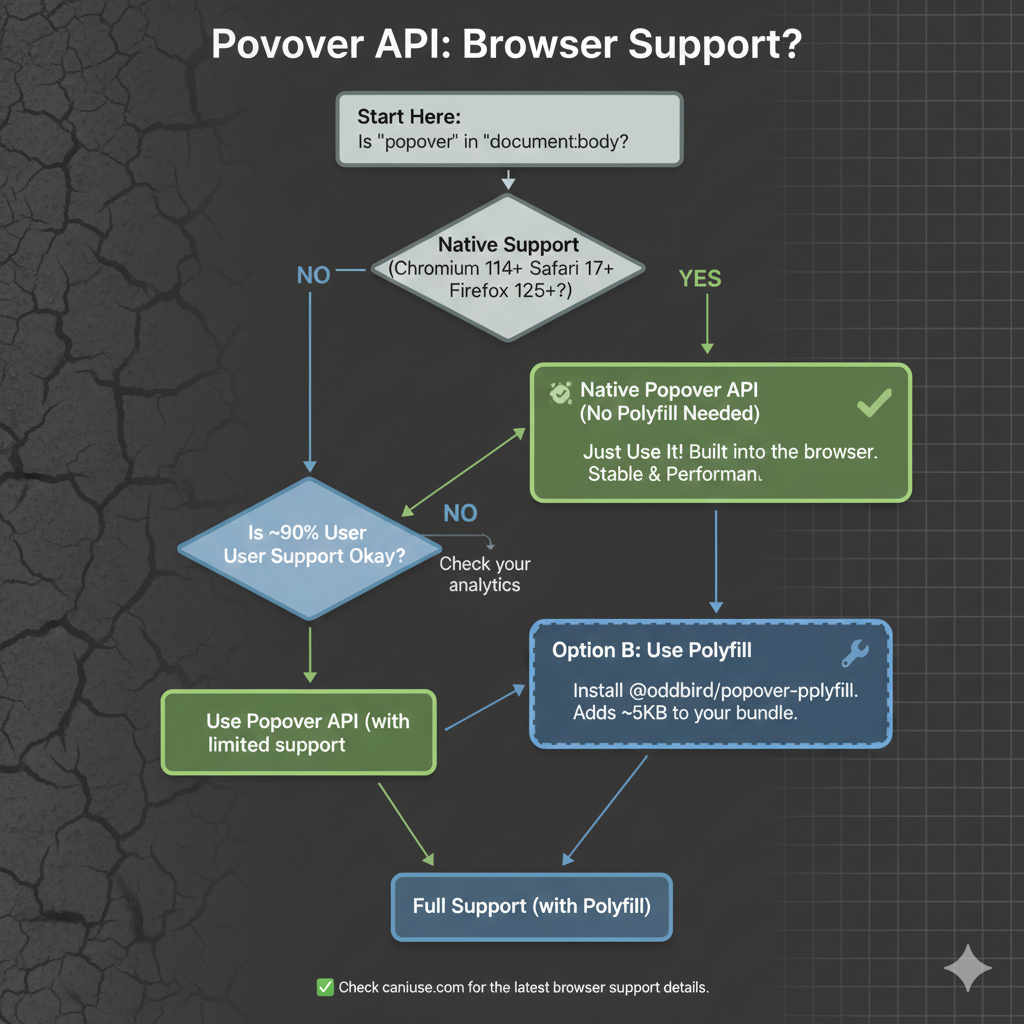
As we start, it’s worth noting that, as with any new feature, there are some things with it that are still being ironed out. That said, it currently enjoys great browser support, although there are several pieces to the overall API that are in flux. It’s worth keeping an eye on Caniuse in the meantime.
The “Old” TooltipBefore the Popover API, using a tooltip library was not a shortcut. It was the default. Browsers didn’t have a native concept of a tooltip that worked across mouse, keyboard, and assistive technology. If you cared about correctness, your only option was to use a library, and that is exactly what I did.
At a high level, the pattern was always the same: a trigger element, a hidden tooltip element, and JavaScript to coordinate the two.
<button class="info">?</button>
<div class="tooltip" role="tooltip">Helpful text</div>
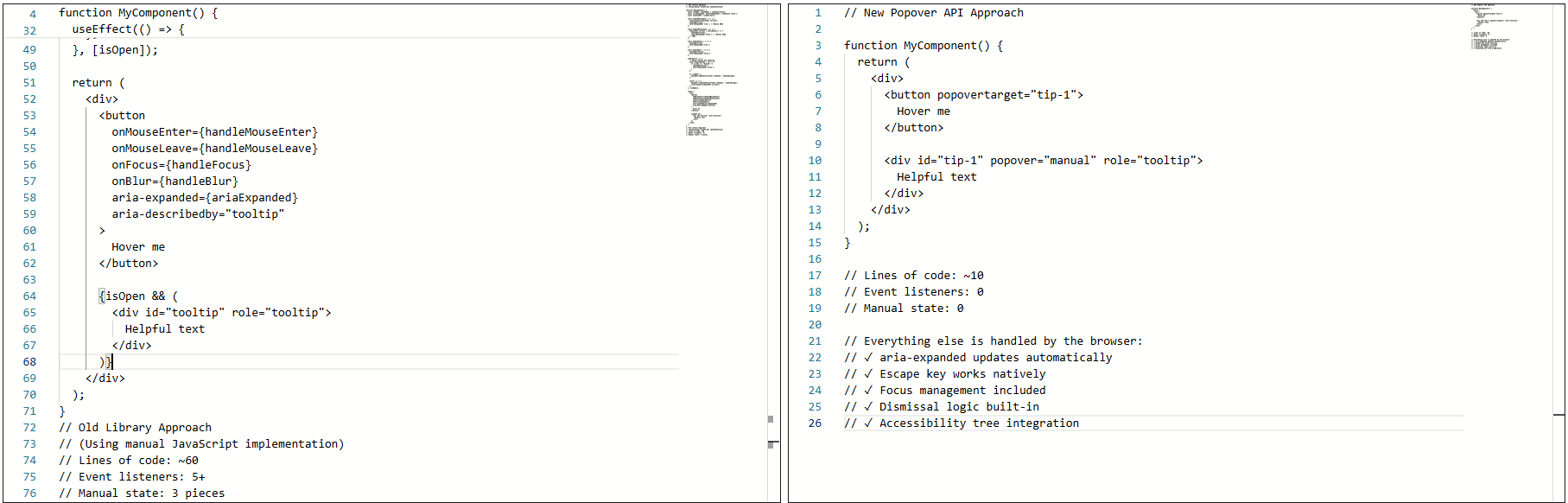
The library handled the wiring that allowed the element to show on hover or focus, hide on blur or mouse leave, and reposition/resize on scroll.
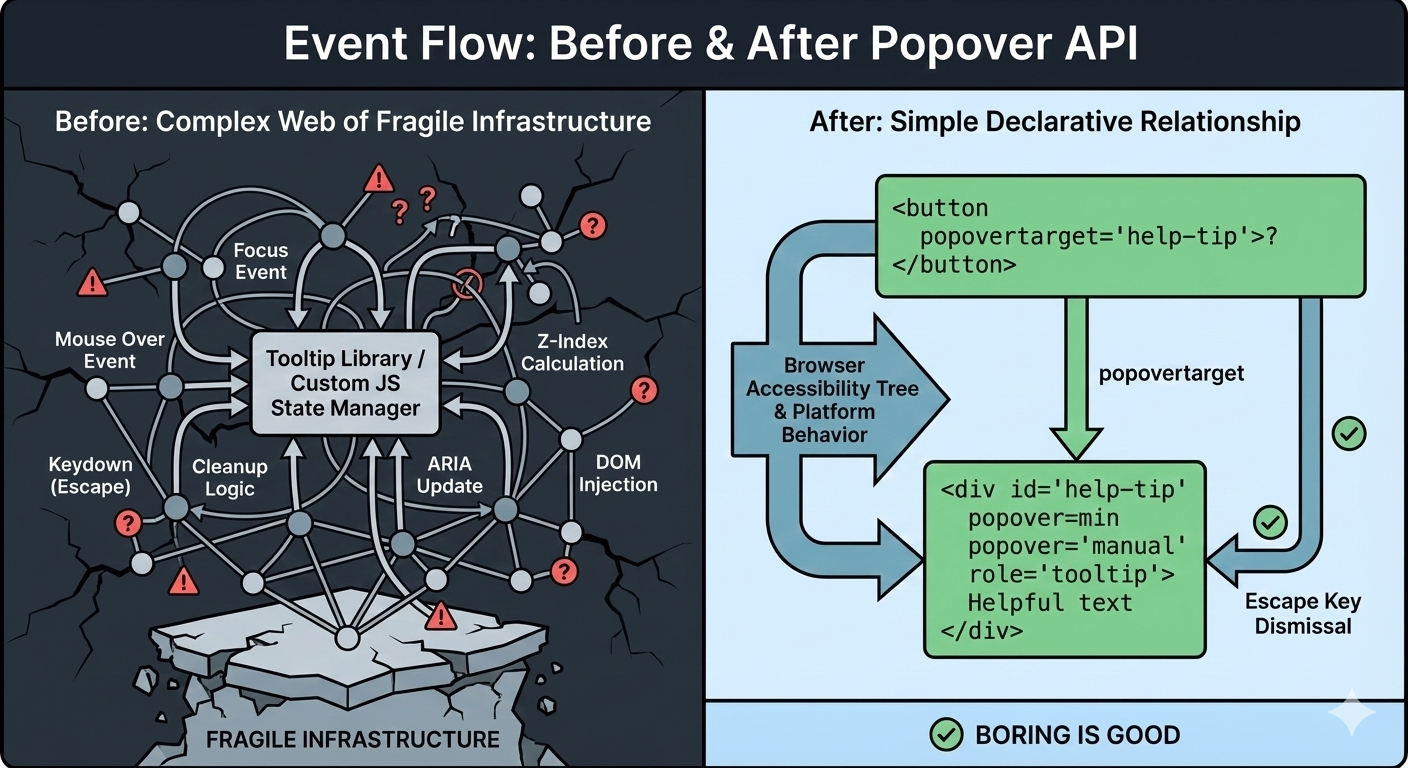
Over time, the tooltip could become fragile. Small changes carried risk. Minor fixes caused regressions. Worse, adding new tooltips inherited the same complexity. Things technically worked, but never felt settled or complete.
That was the state of things when I decided to rebuild the tooltip using the browser’s native Popover API.
The Moment I Tried The Popover APII didn’t switch to using the Popover API because I wanted to experiment with something new. I switched because I was tired of maintaining tooltip behavior that I believed the browser should have already understood.
I was skeptical at first. Most new web APIs promise simplicity, but still require glue, edge-case handling, or fallback logic that quietly recreates the same complexity that you were trying to escape.
So, I tried the Popover API in the smallest way possible. Here’s what that looked like:
<!-- popovertarget creates the connection to id="tip-1" -->
<button popovertarget="tip-1">?</button>
<!-- popover="manual": browser manages this as a popover -->
<!-- role="tooltip": tells assistive technology what this is -->
<div id="tip-1" popover="manual" role="tooltip">
This button triggers a helpful tip.
</div>
1. The Keyboard “Just Works”
Keyboard support depended on multiple layers lining up correctly: focus had to trigger the tooltip, blur had to hide it, Esc had to be wired manually, and timing mattered. If you missed one edge case, the tooltip would either stay open too long or disappear before it could be read.
With the popover attribute set to auto or manual, the browser takes over the basics: Tab and Shift+Tab behave normally, Esc closes the tooltip every time, and no extra listeners are required.
<div popover="manual">
Helpful explanation
</div>
What disappeared from my codebase were global keydown handlers, Esc-specific cleanup logic, and state checks during keyboard navigation. The keyboard experience stopped being something I had to maintain, and it became a browser guarantee.
2. Screenreader Predictability
This was the biggest improvement. Even with careful ARIA work, the behavior varied, as I outlined earlier. Every small change felt risky. Using a popover with a proper role looks and feels a lot more stable and predictable as far as what’s going to happen:
<div popover="manual" role="tooltip">
Helpful explanation
</div>
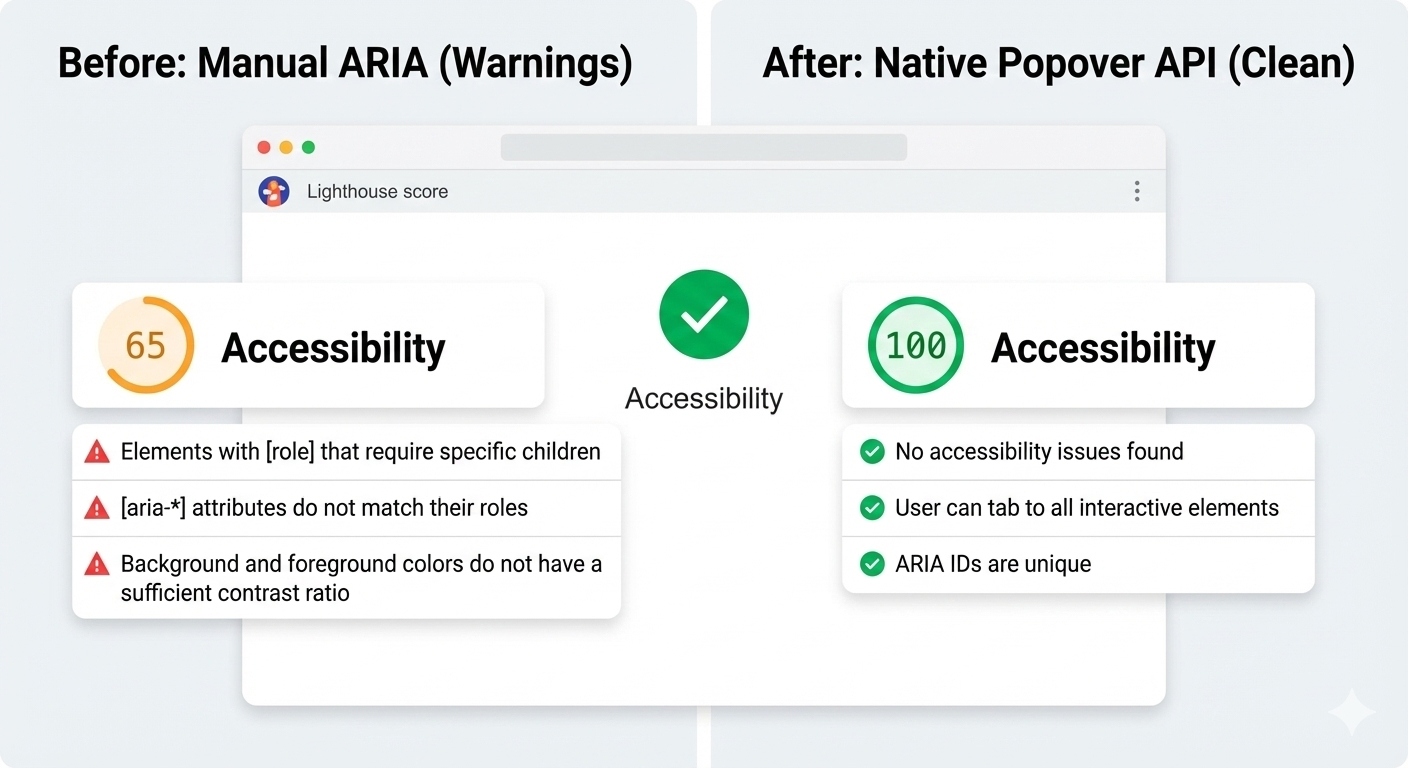
And here’s another win: After the switch, Lighthouse stopped flagging incorrect ARIA state warnings for the interaction, largely because there are no longer custom ARIA states for me to accidentally get wrong.
3. Focus Management
Focus used to be fragile. Before, I had rules like: let focus trigger show tooltip, move focus into tooltip and don’t close, blur trigger when it’s too close, and close tooltip and restore focus manually. This worked until it didn’t.
With the Popover API, the browser enforces a simpler model where focus can more naturally move into the popover. Closing the popover returns focus to the trigger, and there are no invisible focus traps or lost focus moments. And I didn’t add focus restoration code; I removed it.
The Popover API means that tooltips are no longer something you simulate. They’re something the browser understands. Opening, closing, keyboard behavior, Escape handling, and a big chunk of accessibility now come from the platform itself, not from ad-hoc JavaScript.
That does not mean tooltip libraries are obsolete because they still make sense for complex design systems, heavy customization, or legacy constraints, but the default has shifted. For the first time, the simplest tooltip can also be the most correct one. If you are curious, try this experiment: Simply replace just one tooltip in your product with the Popover API, do not rewrite everything, do not migrate a whole system, and just pick one and see what disappears from your code.
When the platform gives you a better primitive, the win is not just fewer lines of JavaScript, but it is fewer things you have to worry about at all.
Check out the full source code in my GitHub repo.
Further Reading
For deeper dives into popovers and related APIs:
- “Poppin’ In”, Geoff Graham
- “Clarifying the Relationship Between Popovers and Dialogs”, Zell Liew
- “What is popover=hint?”, Una Kravets
- “Invoker Commands”, Daniel Schwarz
- “Creating an Auto-Closing Notification with an HTML Popover”, Preethi
- Open UI Popover API Explainer
- “Pop(over) the Balloons”, John Rhea
- “CSS Anchor Positioning”, Juan Diego Rodríguez
MDN also offers comprehensive technical documentation for the Popover API.


 See demo on
See demo on